Eigenvalues and Eigenvectors
An eigenvalues and eigenvectors of the square matrix A are a scalar λ and a nonzero vector v that satisfy
Av = λv
In this equation, A is a n-by-n matrix, v is non-zero n-by-1 vector, and λ is the scalar (which might be either real or complex). Any value of the λ for which this equation has a solution known as eigenvalues of the matrix A. It is also called the characteristic value. The vector, v, which corresponds to this equation, is called eigenvectors. The eigenvalues problem can be written as
A·v-λ·v=0
A·v-λ·I·v=0
(A-λ·I)·v=0
If vis a non-zero, this equation will only have the solutions if
|A-λ·I|=0
This equation is called the characteristic equations of A, and is a nth order polynomial in λ with n roots. These roots are called the eigenvalue of A. We will only handle the case of n distinct roots; through which they may be repeated. For each eigenvalue, there will be eigenvectors for which the eigenvalue equations are true.
Example: Find Eigenvalues and Eigenvectors of the 2×2 Matrix

All that’s left is to find two eigenvectors. Let’s find the eigenvector, v1, connected with the eigenvalue, λ1=-1, first.


In this case, we find that the first eigenvector is any 2 component column vector in which the two items have equal magnitude and opposite sign.

where k1 is an arbitrary constant. If we didn’t have to use +1 and -1, we have used any two quantities of equal magnitude and opposite sign.
Going through the same process for the second eigenvalue:
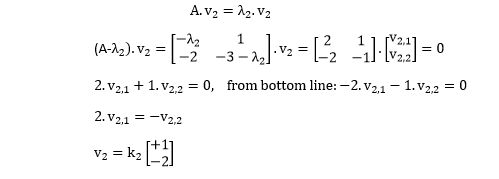
Again, the choice of the +1 and -2 for the eigenvectors was arbitrary; only their ratio is essential. This is demonstrating in the MATLAB code below.

Note: MATLAB chooses different equations for the eigenvector than the ones we chose. The ratio of v1,1 to v1,2, and the ratios of v2,1 to v2,2 are similar to our solution; the chosen eigenvector of the system is not unique, but the ratio of their components is. MATLAB chooses the values such that sum of the square of the components of each eigenvector equals unity.
