The easiest way to find the probability from a z-score is to simply look up the probability that corresponds to the z-score in the z table.
This tutorial explains how to use the z table to find the following probabilities:
- The probability of a value being less than a certain z-score.
- The probability of a value being greater than a certain z-score.
- The probability of a value being between two certain z-scores.
Let’s jump in!
Example 1: Probability Less Than a Certain Z-Score
Suppose we would like to find the probability that a value in a given distribution has a z-score less than z = 0.25.
To find this probability, we need to look up 0.25 in the z-table:

The probability that a value in a given distribution has a z-score less than z = 0.25 is approximately 0.5987.
Note: This could also be written as 59.87% in percentage terms.
Example 2: Probability Greater Than a Certain Z-Score
Suppose we would like to find the probability that a value in a given distribution has a z-score greater than z = -0.5.
To find this probability, we need to look up -0.5 in the z-table:
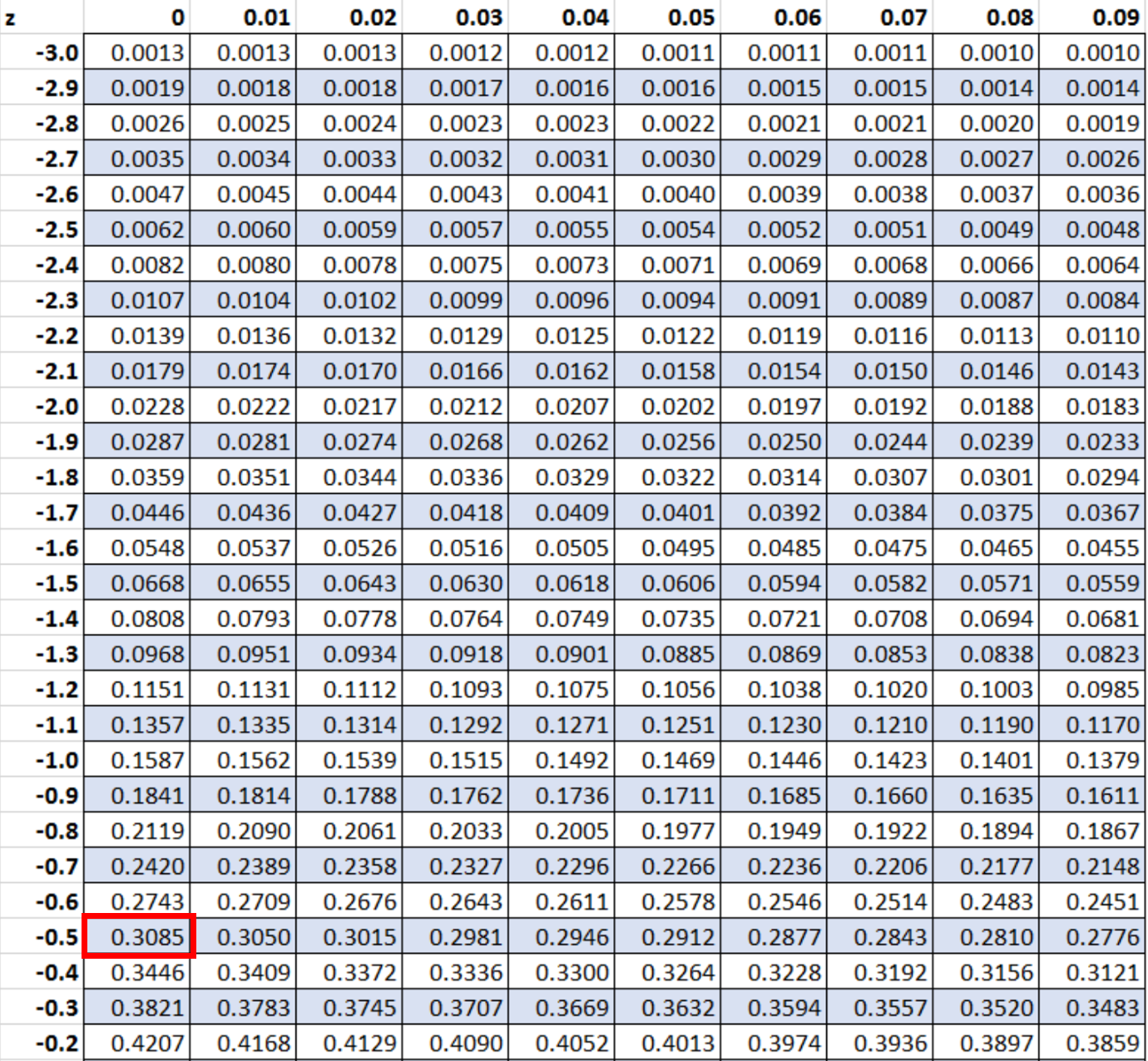
The probability that corresponds to a z-score of -0.5 is .3085.
However, since we want to know the probability that a value in a given distribution has a z-score greater than -0.5, we need to subtract this probability from 1.
Thus, the probability that a value in a given distribution has a z-score greater than -0.5 is: 1 – .3085 = 0.6915.
Example 3: Probability Between Two Z-Scores
Suppose we would like to find the probability that a value in a given distribution has a z-score between z = 0.4 and z = 1.
First, we will look up the value 0.4 in the z-table:
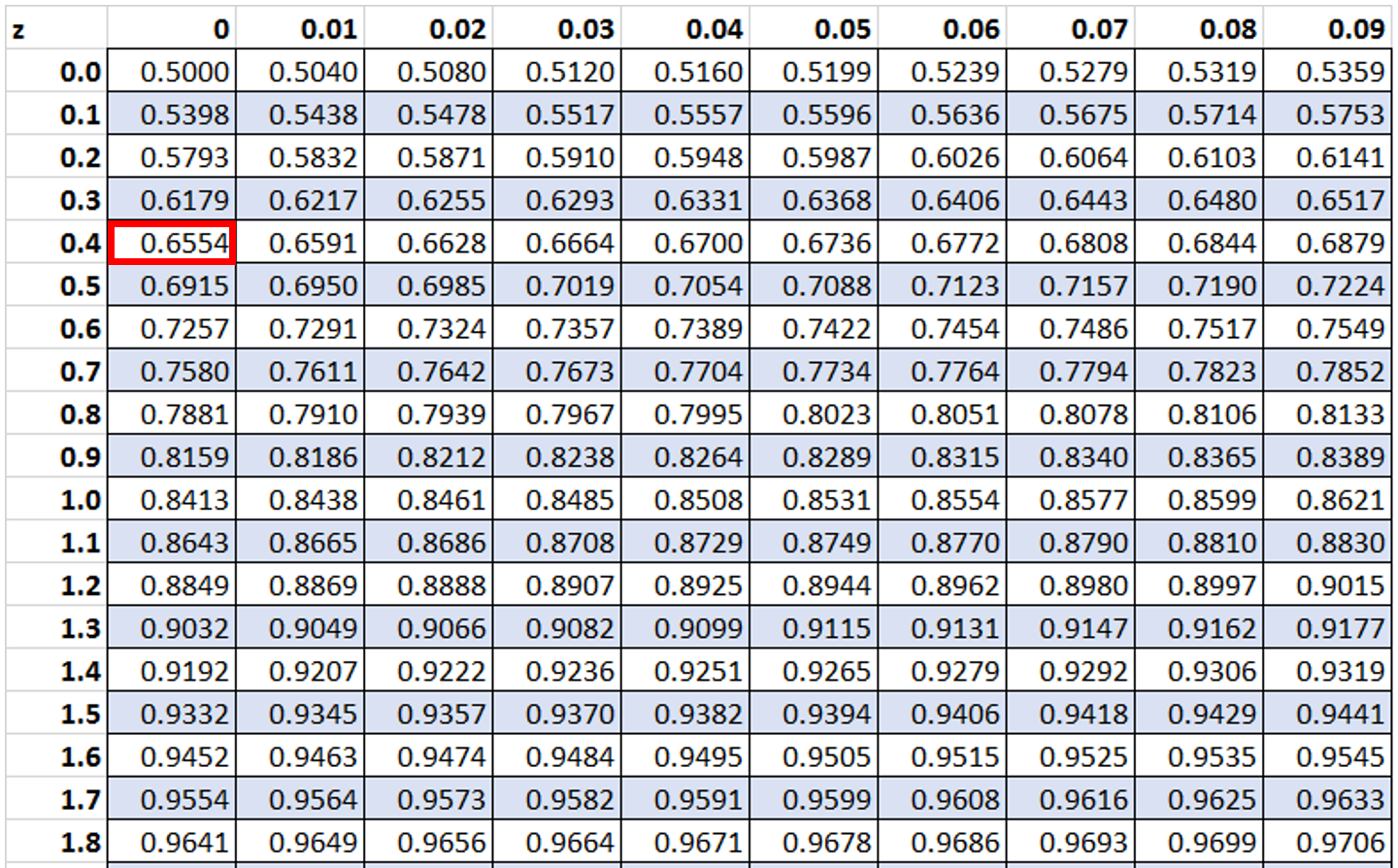
Then, we will look up the value 1 in the z-table:
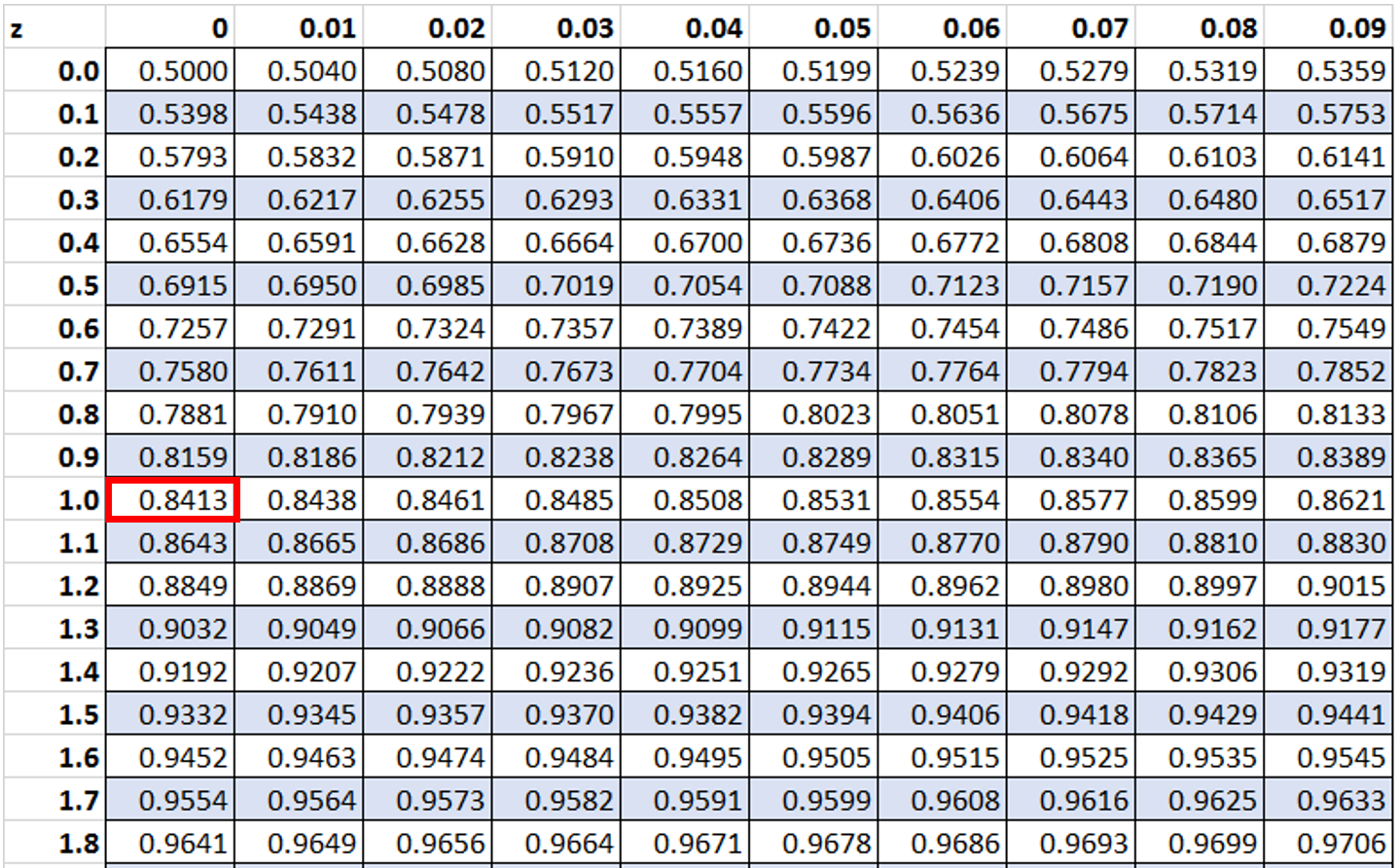
Then we will subtract the smaller value from the larger value: 0.8413 – 0.6554 = 0.1859.
Thus, the probability that a value in a given distribution has a z-score between z = 0.4 and z = 1 is approximately 0.1859.
Additional Resources
The following tutorials provide additional information about z-scores:
5 Examples of Using Z-Scores in Real Life
How to Convert Z-Scores to Raw Scores
How to Find Z-Scores Given Area
