Hill Cipher Program in Java

In classical cryptography, the hill cipher is a polygraphic substitution cipher based on Linear Algebra. It was invented by Lester S. Hill in the year 1929. In simple words, it is a cryptography algorithm used to encrypt and decrypt data for the purpose of data security.

The algorithm uses matrix calculations used in Linear Algebra. It is easier to understand if we have the basic knowledge of matrix multiplication, modulo calculation, and the inverse calculation of matrices.

In hill cipher algorithm every letter (A-Z) is represented by a number moduli 26. Usually, the simple substitution scheme is used where A = 0, B = 1, C = 2…Z = 25 in order to use 2×2 key matrix.

Note: The complexity of the algorithm increases with the size of the key matrix.

Encryption

To encrypt the text using hill cipher, we need to perform the following operation.

Where K is the key matrix and P is plain text in vector form. Matrix multiplication of K and P generates the encrypted ciphertext.

Steps For Encryption

Step 1: Let’s say our key text (2×2) is DCDF. Convert this key using a substitution scheme into a 2×2 key matrix as shown below:

Hill Cipher Program in Java

Step 2: Now, we will convert our plain text into vector form. Since the key matrix is 2×2, the vector must be 2×1 for matrix multiplication. (Suppose the key matrix is 3×3, a vector will be a 3×1 matrix.)

In our case, plain text is TEXT that is four letters long word; thus we can put in a 2×1 vector and then substitute as:

Hill Cipher Program in Java

Step 3: Multiply the key matrix with each 2×1 plain text vector, and take the modulo of result (2×1 vectors) by 26. Then concatenate the results, and we get the encrypted or ciphertext as RGWL.

Hill Cipher Program in Java

Decryption

To encrypt the text using hill cipher, we need to perform the following operation.

Where K is the key matrix and C is the ciphertext in vector form. Matrix multiplication of inverse of key matrix K and ciphertext C generates the decrypted plain text.

Steps For Decryption

Step 1: Calculate the inverse of the key matrix. First, we need to find the determinant of the key matrix (must be between 0-25). Here the Extended Euclidean algorithm is used to get modulo multiplicative inverse of key matrix determinant

Hill Cipher Program in Java

Step 2: Now, we multiply the 2×1 blocks of ciphertext and the inverse of the key matrix. The resultant block after concatenation is the plain text that we have encrypted i.e., TEXT.

Hill Cipher Program in Java

Let’s see an example.

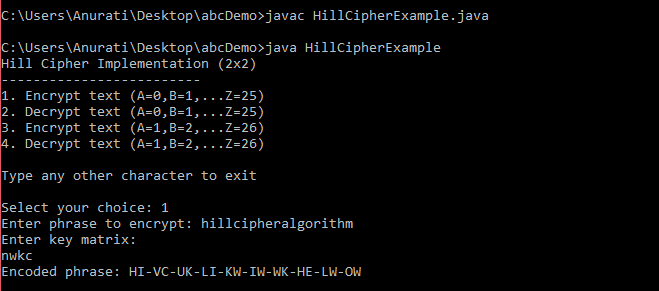
Consider the following program in which we have performed the hill cipher encryption and decrpytion on a 2 x 2 matrix. Here, we follow both the substitution schemes, A = 0, B = 1,… and A = 1, B = 2,…

HillCipherExample.java

  import java.util.ArrayList;  import java.util.Scanner;  public class HillCipherExample {      //method to accept key matrix      private static int[][] getKeyMatrix() {          Scanner sc = new Scanner(System.in);          System.out.println(“Enter key matrix:”);          String key = sc.nextLine();          //int len = key.length();          double sq = Math.sqrt(key.length());          if (sq != (long) sq) {              System.out.println(“Cannot Form a square matrix”);          }          int len = (int) sq;          int[][] keyMatrix = new int[len][len];          int k = 0;          for (int i = 0; i < len; i++)          {              for (int j = 0; j < len; j++)              {                  keyMatrix[i][j] = ((int) key.charAt(k)) – 97;                  k++;              }          }          return keyMatrix;      }      // Below method checks whether the key matrix is valid (det=0)      private static void isValidMatrix(int[][] keyMatrix) {          int det = keyMatrix[0][0] * keyMatrix[1][1] – keyMatrix[0][1] * keyMatrix[1][0];          // If det=0, throw exception and terminate          if(det == 0) {              throw new java.lang.Error(“Det equals to zero, invalid key matrix!”);          }      }      // This method checks if the reverse key matrix is valid (matrix mod26 = (1,0,0,1)          private static void isValidReverseMatrix(int[][] keyMatrix, int[][] reverseMatrix) {          int[][] product = new int[2][2];          // Find the product matrix of key matrix times reverse key matrix          product[0][0] = (keyMatrix[0][0]*reverseMatrix[0][0] + keyMatrix[0][1] * reverseMatrix[1][0]) % 26;          product[0][1] = (keyMatrix[0][0]*reverseMatrix[0][1] + keyMatrix[0][1] * reverseMatrix[1][1]) % 26;          product[1][0] = (keyMatrix[1][0]*reverseMatrix[0][0] + keyMatrix[1][1] * reverseMatrix[1][0]) % 26;          product[1][1] = (keyMatrix[1][0]*reverseMatrix[0][1] + keyMatrix[1][1] * reverseMatrix[1][1]) % 26;          // Check if a=1 and b=0 and c=0 and d=1          // If not, throw exception and terminate          if(product[0][0] != 1 || product[0][1] != 0 || product[1][0] != 0 || product[1][1] != 1) {              throw new java.lang.Error(“Invalid reverse matrix found!”);          }      }      // This method calculates the reverse key matrix      private static int[][] reverseMatrix(int[][] keyMatrix) {          int detmod26 = (keyMatrix[0][0] * keyMatrix[1][1] – keyMatrix[0][1] * keyMatrix[1][0]) % 26; // Calc det          int factor;          int[][] reverseMatrix = new int[2][2];          // Find the factor for which is true that          // factor*det = 1 mod 26          for(factor=1; factor < 26; factor++)          {              if((detmod26 * factor) % 26 == 1)              {                  break;              }          }          // Calculate the reverse key matrix elements using the factor found          reverseMatrix[0][0] = keyMatrix[1][1]           * factor % 26;          reverseMatrix[0][1] = (26 – keyMatrix[0][1])    * factor % 26;          reverseMatrix[1][0] = (26 – keyMatrix[1][0])    * factor % 26;          reverseMatrix[1][1] = keyMatrix[0][0]           * factor % 26;          return reverseMatrix;      }      // This method echoes the result of encrypt/decrypt      private static void echoResult(String label, int adder, ArrayList<Integer> phrase) {          int i;          System.out.print(label);          // Loop for each pair          for(i=0; i < phrase.size(); i += 2) {              System.out.print(Character.toChars(phrase.get(i) + (64 + adder)));              System.out.print(Character.toChars(phrase.get(i+1) + (64 + adder)));              if(i+2 <phrase.size()) {                  System.out.print(“-“);              }          }          System.out.println();      }      // This method makes the actual encryption       public static void encrypt(String phrase, boolean alphaZero)      {          int i;          int adder = alphaZero ? 1 : 0; // For calclulations depending on the alphabet          int[][] keyMatrix;          ArrayList<Integer> phraseToNum = new ArrayList<>();          ArrayList<Integer> phraseEncoded = new ArrayList<>();          // Delete all non-english characters, and convert phrase to upper case          phrase = phrase.replaceAll(“[^a-zA-Z]”,””).toUpperCase();            // If phrase length is not an even number, add “Q” to make it even          if(phrase.length() % 2 == 1) {              phrase += “Q”;          }          // Get the 2×2 key matrix from sc          keyMatrix = getKeyMatrix();          // Check if the matrix is valid (det != 0)          isValidMatrix(keyMatrix);          // Convert characters to numbers according to their          // place in ASCII table minus 64 positions (A=65 in ASCII table)          // If we use A=0 alphabet, subtract one more (adder)          for(i=0; i < phrase.length(); i++) {              phraseToNum.add(phrase.charAt(i) – (64 + adder));          }          // Find the product per pair of the phrase with the key matrix modulo 26          // If we use A=1 alphabet and result is 0, replace it with 26 (Z)          for(i=0; i < phraseToNum.size(); i += 2) {              int x = (keyMatrix[0][0] * phraseToNum.get(i) + keyMatrix[0][1] * phraseToNum.get(i+1)) % 26;              int y = (keyMatrix[1][0] * phraseToNum.get(i) + keyMatrix[1][1] * phraseToNum.get(i+1)) % 26;              phraseEncoded.add(alphaZero ? x : (x == 0 ? 26 : x ));              phraseEncoded.add(alphaZero ? y : (y == 0 ? 26 : y ));          }          // Print the result          echoResult(“Encoded phrase: “, adder, phraseEncoded);      }      // This method makes the actual decryption      public static void decrypt(String phrase, boolean alphaZero)      {          int i, adder = alphaZero ? 1 : 0;          int[][] keyMatrix, revKeyMatrix;          ArrayList<Integer> phraseToNum = new ArrayList<>();          ArrayList<Integer> phraseDecoded = new ArrayList<>();          // Delete all non-english characters, and convert phrase to upper case          phrase = phrase.replaceAll(“[^a-zA-Z]”,””).toUpperCase();            // Get the 2×2 key matrix from sc          keyMatrix = getKeyMatrix();          // Check if the matrix is valid (det != 0)          isValidMatrix(keyMatrix);          // Convert numbers to characters according to their          // place in ASCII table minus 64 positions (A=65 in ASCII table)          // If we use A=0 alphabet, subtract one more (adder)          for(i=0; i < phrase.length(); i++) {              phraseToNum.add(phrase.charAt(i) – (64 + adder));          }          // Find the reverse key matrix          revKeyMatrix = reverseMatrix(keyMatrix);          // Check if the reverse key matrix is valid (product = 1,0,0,1)          isValidReverseMatrix(keyMatrix, revKeyMatrix);          // Find the product per pair of the phrase with the reverse key matrix modulo 26          for(i=0; i < phraseToNum.size(); i += 2) {              phraseDecoded.add((revKeyMatrix[0][0] * phraseToNum.get(i) + revKeyMatrix[0][1] * phraseToNum.get(i+1)) % 26);              phraseDecoded.add((revKeyMatrix[1][0] * phraseToNum.get(i) + revKeyMatrix[1][1] * phraseToNum.get(i+1)) % 26);          }          // Print the result          echoResult(“Decoded phrase: “, adder, phraseDecoded);      }      //main method      public static void main(String[] args) {          String opt, phrase;          byte[] p;          Scanner sc = new Scanner(System.in);          System.out.println(“Hill Cipher Implementation (2×2)”);          System.out.println(“————————-“);          System.out.println(“1. Encrypt text (A=0,B=1,…Z=25)”);          System.out.println(“2. Decrypt text (A=0,B=1,…Z=25)”);          System.out.println(“3. Encrypt text (A=1,B=2,…Z=26)”);          System.out.println(“4. Decrypt text (A=1,B=2,…Z=26)”);          System.out.println();          System.out.println(“Type any other character to exit”);          System.out.println();          System.out.print(“Select your choice: “);          opt = sc.nextLine();          switch (opt)          {              case “1”:                  System.out.print(“Enter phrase to encrypt: “);                  phrase = sc.nextLine();                  encrypt(phrase, true);                  break;              case “2”:                  System.out.print(“Enter phrase to decrypt: “);                  phrase = sc.nextLine();                  decrypt(phrase, true);                  break;              case “3”:                  System.out.print(“Enter phrase to encrypt: “);                  phrase = sc.nextLine();                  encrypt(phrase, false);                  break;              case “4”:                  System.out.print(“Enter phrase to decrypt: “);                  phrase = sc.nextLine();                  decrypt(phrase, false);                  break;          }      }  }  

Output:

Hill Cipher Program in Java

Next TopicLazy Loading in Java

Hill Cipher Program in Java

Hill Cipher Program in Java

Note: The complexity of the algorithm increases with the size of the key matrix.

Encryption

Steps For Encryption

Decryption

Steps For Decryption

Generating QR Code in Java

How to Find Array Length in Java

You may also like