Multiple linear regression is a method we can use to quantify the relationship between two or more predictor variables and a response variable.
This tutorial explains how to perform multiple linear regression by hand.
Example: Multiple Linear Regression by Hand
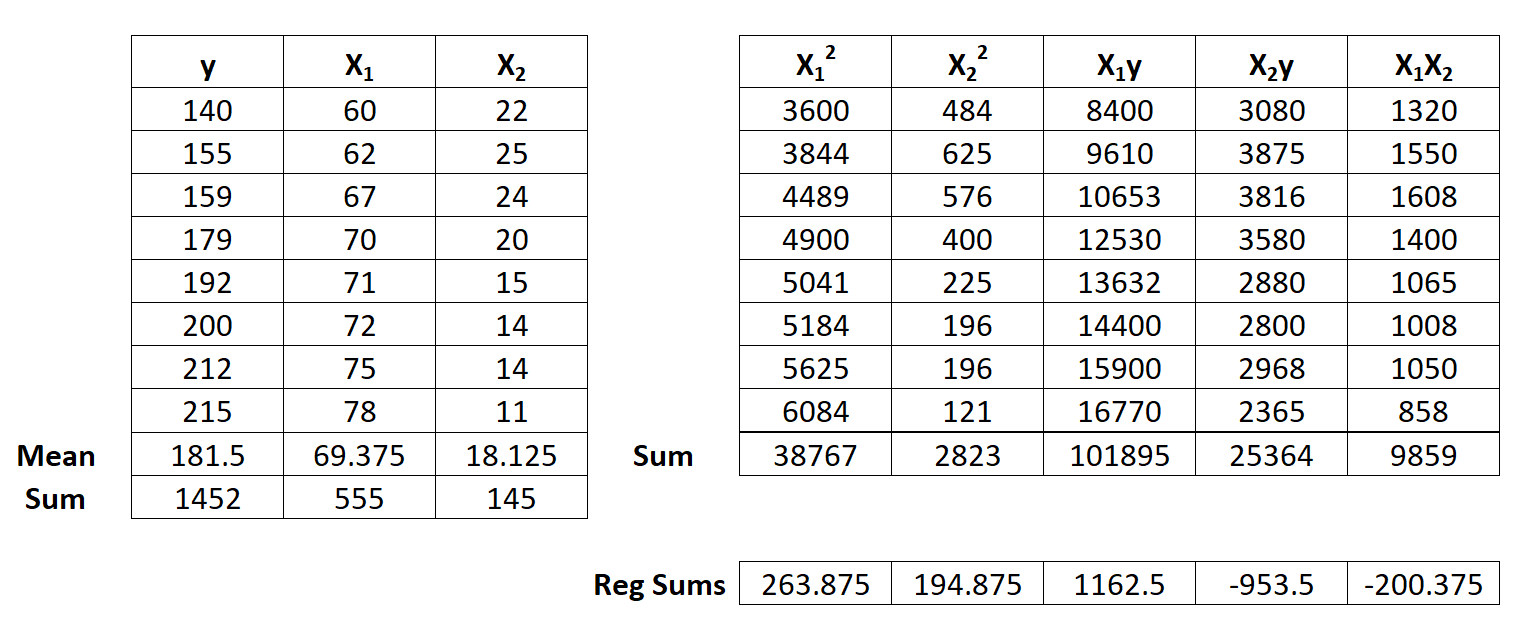
Suppose we have the following dataset with one response variable y and two predictor variables X1 and X2:

Use the following steps to fit a multiple linear regression model to this dataset.
Step 1: Calculate X12, X22, X1y, X2y and X1X2.

Step 2: Calculate Regression Sums.
Next, make the following regression sum calculations:
- Σx12 = ΣX12 – (ΣX1)2 / n = 38,767 – (555)2 / 8 = 263.875
- Σx22 = ΣX22 – (ΣX2)2 / n = 2,823 – (145)2 / 8 = 194.875
- Σx1y = ΣX1y – (ΣX1Σy) / n = 101,895 – (555*1,452) / 8 = 1,162.5
- Σx2y = ΣX2y – (ΣX2Σy) / n = 25,364 – (145*1,452) / 8 = -953.5
- Σx1x2 = ΣX1X2 – (ΣX1ΣX2) / n = 9,859 – (555*145) / 8 = -200.375
Step 3: Calculate b0, b1, and b2.
The formula to calculate b1 is: [(Σx22)(Σx1y) – (Σx1x2)(Σx2y)] / [(Σx12) (Σx22) – (Σx1x2)2]
Thus, b1 = [(194.875)(1162.5) – (-200.375)(-953.5)] / [(263.875) (194.875) – (-200.375)2] = 3.148
The formula to calculate b2 is: [(Σx12)(Σx2y) – (Σx1x2)(Σx1y)] / [(Σx12) (Σx22) – (Σx1x2)2]
Thus, b2 = [(263.875)(-953.5) – (-200.375)(1152.5)] / [(263.875) (194.875) – (-200.375)2] = -1.656
The formula to calculate b0 is: y – b1X1 – b2X2
Thus, b0 = 181.5 – 3.148(69.375) – (-1.656)(18.125) = -6.867
Step 5: Place b0, b1, and b2 in the estimated linear regression equation.
The estimated linear regression equation is: ŷ = b0 + b1*x1 + b2*x2
In our example, it is ŷ = -6.867 + 3.148x1 – 1.656x2
How to Interpret a Multiple Linear Regression Equation
Here is how to interpret this estimated linear regression equation: ŷ = -6.867 + 3.148x1 – 1.656x2
b0 = -6.867. When both predictor variables are equal to zero, the mean value for y is -6.867.
b1 = 3.148. A one unit increase in x1 is associated with a 3.148 unit increase in y, on average, assuming x2 is held constant.
b2 = -1.656. A one unit increase in x2 is associated with a 1.656 unit decrease in y, on average, assuming x1 is held constant.
Additional Resources
An Introduction to Multiple Linear Regression
How to Perform Simple Linear Regression by Hand
