To find the percentile of a z-score on a TI-84 calculator, you can use the following syntax:
normalcdf(-99, z-score, μ, σ)
where:
- μ = population mean
- σ = population standard deviation
To access this function on a TI-84 calculator, simply press 2nd then press VARS then scroll down to normalcdf( and press ENTER.

The following examples show how to use this function in practice.
Example 1: Find Percentile of a Negative Z-Score
Suppose we would like to find the percentile that corresponds to a z-score of -1.44.
We can use the following syntax on a TI-84 calculator to find this percentile:
normalcdf(-99, -1.44, 0, 1) Note: We use -99 as the “lower bound” to simulate a value of negative infinity.
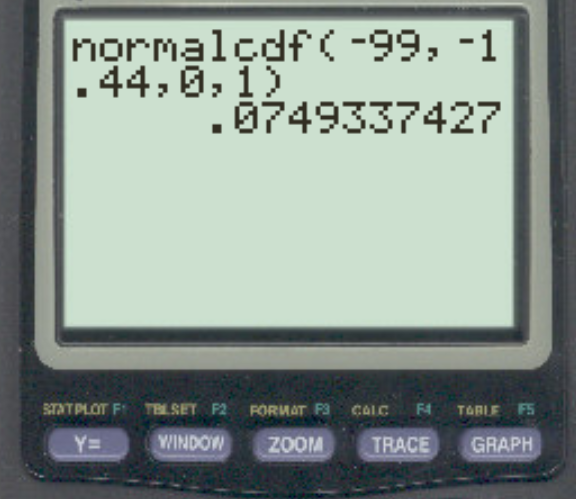
The percentile that corresponds to a z-score of -1.44 is 0.0749. This means that only 7.49% of values in the normal distribution fall below a z-score of -1.44.
Example 2: Find Percentile of a Positive Z-Score
Suppose we would like to find the percentile that corresponds to a z-score of 0.56.
We can use the following syntax on a TI-84 calculator to find this percentile:
normalcdf(-99, 0.56, 0, 1) Once again we use -99 as the “lower bound” to simulate a value of negative infinity.
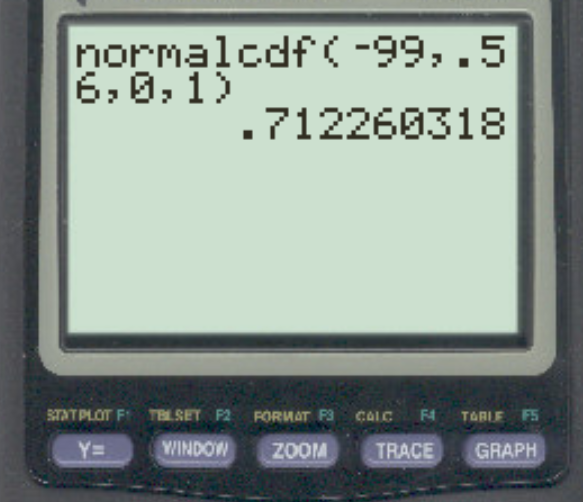
The percentile that corresponds to a z-score of 0.56 is 0.7123. This means that 71.23% of values in the normal distribution fall below a z-score of 0.56.
The Relationship Between Percentiles and Z-Scores
Z-scores can take on any value between negative infinity and infinity. Percentiles, however, can only take on values between 0 and 100.
A z-score of 0 corresponds to a percentile of exactly 0.50. Thus, any z-score greater than 0 corresponds to a percentile greater than 0.50 and any z-score less than 0 corresponds to a percentile less than 0.50.
Additional Resources
How to Calculate Z-Scores on a TI-84 Calculator
How to Find the Z Critical Value on a TI-84 Calculator
