An outlier is an observation that lies abnormally far away from other values in a dataset.
Outliers can be problematic because they can affect the results of an analysis.
However, they can also be informative about the data you’re studying because they can reveal abnormal cases or individuals that have rare traits.
In any analysis, you must decide to remove or keep outliers.
Fortunately, you can use the following flow chart to help you decide:

Let’s take a look a closer look at each question in the flow chart.
Is the Outlier a Result of Data Entry Error?
Sometimes outliers in a dataset are simply a result of data entry error.
For example, suppose a biologist is collecting data on the height of a certain species of plants and records the following data:
- 6.83 inches
- 7.51 inches
- 5.21 inches
- 5.84 inches
- 7.83 inches
- 755 inches
- 6.53 inches
- 6.31 inches
- 5.91 inches
Clearly the entry for 755 inches is an outlier and is likely a result of data entry error. More than likely, the height should have been 7.55 inches but was simply entered incorrectly.
If the biologist kept this observation and calculated a descriptive statistic like the mean height of the plants in the sample, this observation would greatly skew the results and give an inaccurate picture of the true mean height of the plants.
In this scenario (and in scenarios similar to this one) it makes sense to remove this outlier from the dataset because it’s an error and is not a legitimate data point to include in the analysis.
Does the Outlier Significantly Affect the Results of the Analysis?
If an observation is a true outlier and not just a result of a data entry error, then we need to examine whether or not the outlier affects the results of the analysis.
For example, suppose a biologist is studying the relationship between fertilizer and plant height. She wants to fit a simple linear regression model using fertilizer as the predictor variable and plant height as the response variable.
She collects the following data for 12 different plants:
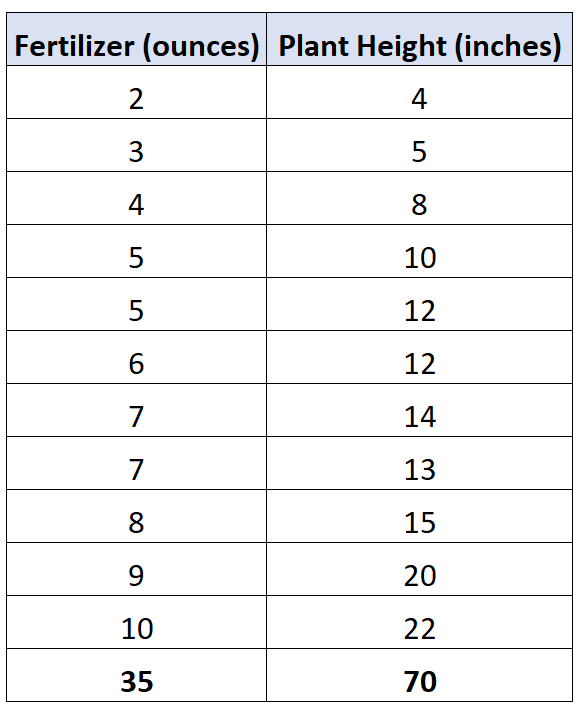
Clearly the last observation is an outlier.
However, if we create a scatterplot to visualize this dataset we can see that the regression line wouldn’t change much whether we included the outlier or not:
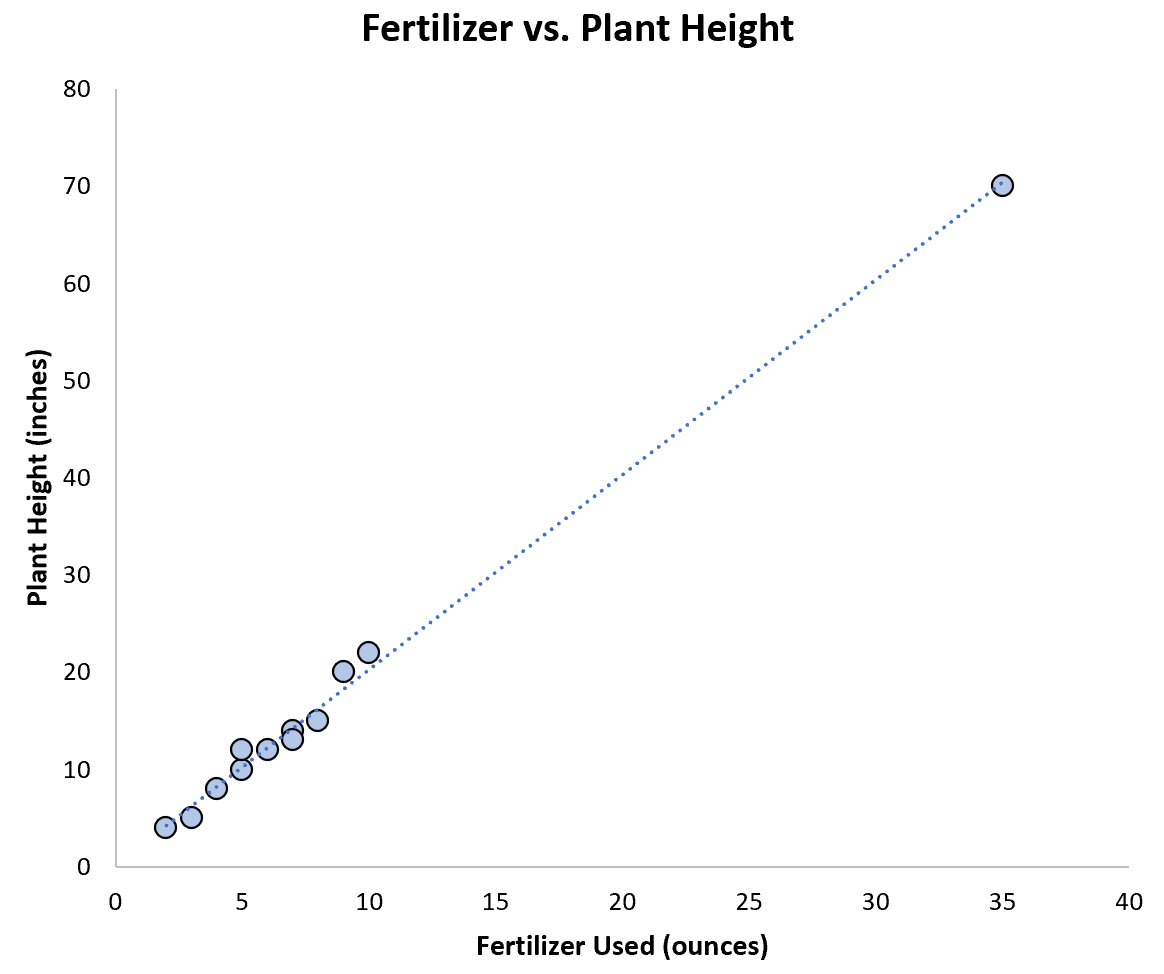
In this scenario, the outlier doesn’t actually violate any of the assumptions of a linear regression model, so we could keep it in the dataset.
However, suppose we had the following outlier in the data:
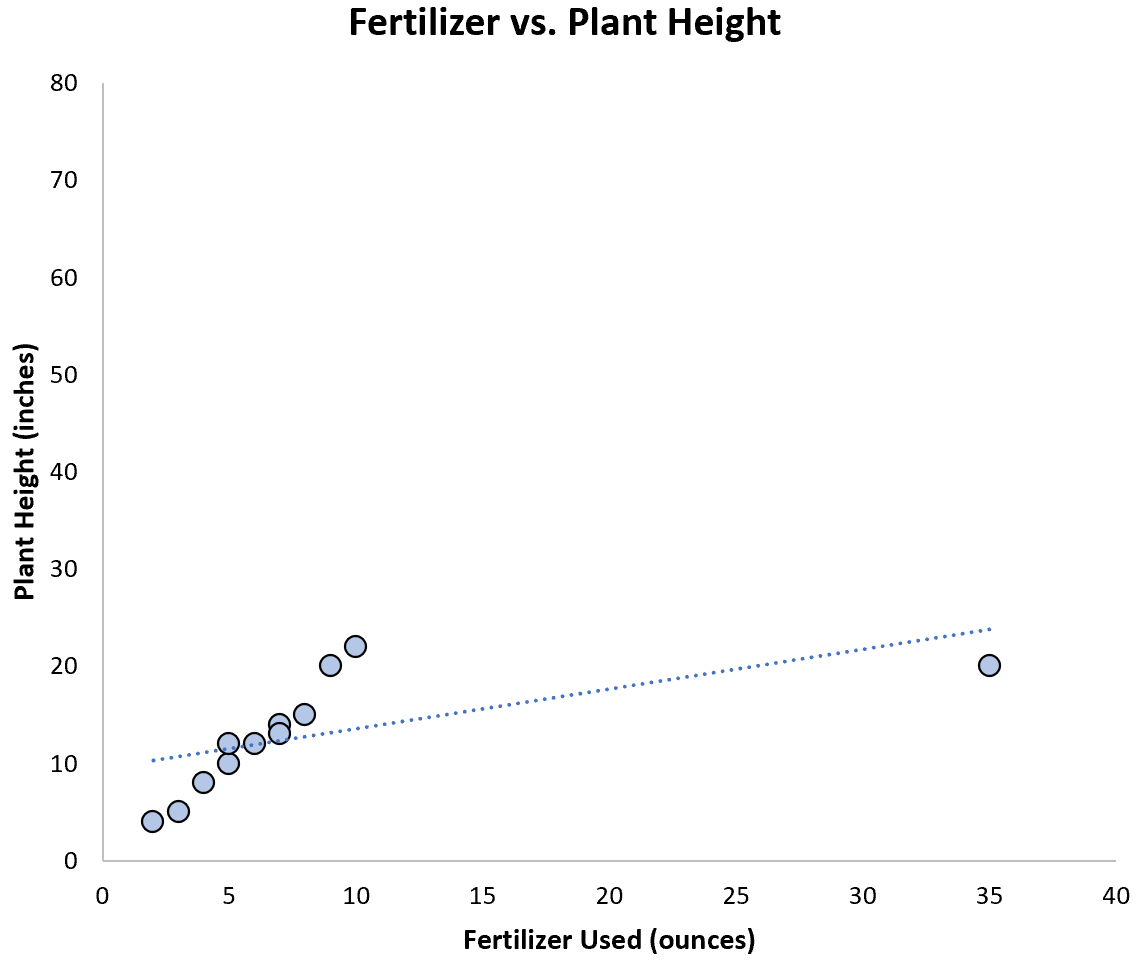
Clearly this outlier significantly affects the regression line so we could fit one regression model with the outlier and one without, then report the results of both regression models.
Does the Outlier Affect the Assumptions Made in the Analysis?
If an outlier is not a result of a data entry error and it does not significantly affect the results of an analysis, then we need to ask whether or not the outlier affects the assumptions made in an analysis.
If it does not affect the assumptions, then we can simply keep it in the data.
However, if it does affect the assumptions then we have a couple options:
1. Remove it. We can simply remove it from the data and make a note of this when reporting the results.
2. Perform a transformation on the data. Instead of removing the outlier, we could try performing a transformation on the data such as taking the square root or the log of all of the data values. This has been shown to shrink outlier values and often makes the data more normally distributed.
No matter how you decide to handle outliers in your data, you should make a note of your decision in the output of your analysis along with your reasoning.
Additional Resources
The following tutorials explain how to find and remove outliers in different statistical software:
How to Find Outliers in Excel
How to Find Outliers in Google Sheets
How to Find Outliers in R
How to Find Outliers in Python
How to Find Outliers in SPSS
