Whenever you come across the term tα/2 in statistics, it is simply referring to the t critical value from the t-distribution table that corresponds to α/2.
This tutorial explains the following:
- How to find tα/2 using a z table.
- How to find tα/2 using a calculator.
- How to use tα/2 values.
Let’s jump in!
How to find tα/2 using a t table
Suppose we want to find tα/2 for some test that is using the following values:
- Alpha Level: 0.10
- Types of test: Two-tailed
- Degrees of freedom: 20
Using a t-distribution table, we can find that the t critical value is 1.725:

How to find tα/2 using a calculator
We can also use the Inverse t Distribution Calculator to find tα/2 for some test.
For example, suppose we once again want to find tα/2 for some test that is using the following values:
- Alpha Level: 0.10
- Types of test: Two-tailed
- Degrees of freedom: 20
We can enter the following values into the calculator and find that the t critical value is 1.7247:
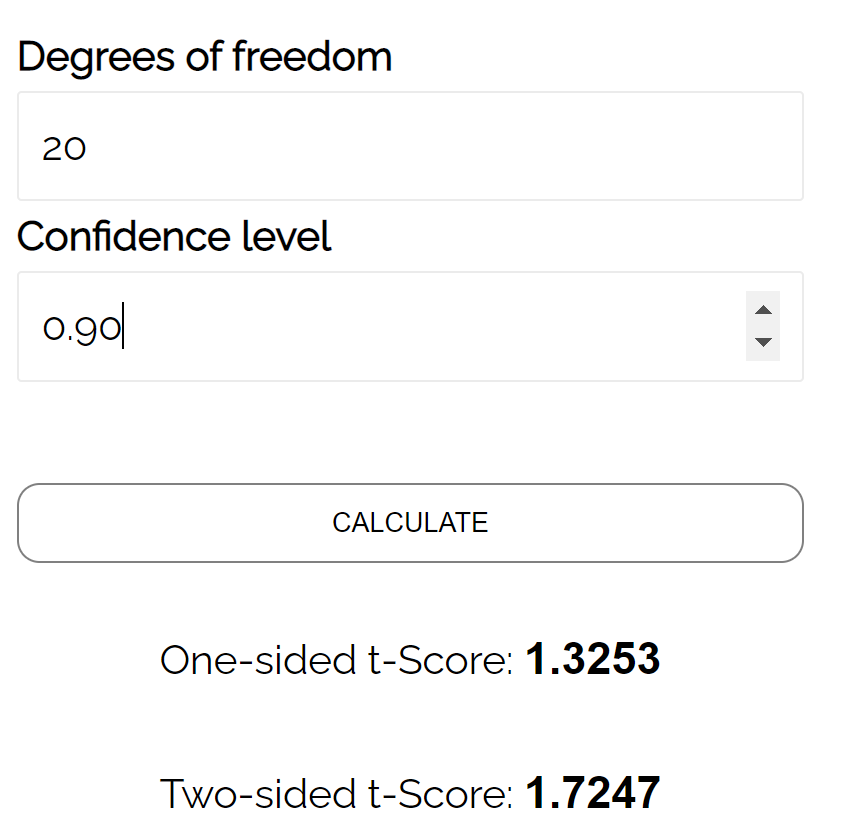
This matches the t critical value that we found in the t distribution table.
How to Use tα/2 Values
In practice, t critical values are used in hypothesis tests to determine whether or not the results of a test are statistically significant.
The basic process for doing so is as follows:
Step 1: Calculate the test statistic using raw data.
Step 2: Compare the test statistic to the t critical value (tα/2).
Step 3: Reject or fail to reject the null hypothesis of the test.
If the absolute value of the t test statistic is greater than the t critical value, then we can reject the null hypothesis of the test.
Otherwise, if the absolute value of the t test statistic is less than the t critical value, then we fail to reject the null hypothesis.
Additional Resources
How to Read the t-Distribution Table
How to Find t Critical Values in Excel
How to Find t Critical Values in R
