In statistics, we’re often interested in understanding how two variables are related to each other. For example, we might want to know:
- What is the relationship between the number of hours a student studies and the exam score they receive?
- What is the relationship between the temperature outside and the number of ice cream bars sold by a food truck?
- What is the relationship between dollars spent on advertising and total income earned for a certain company?
In each scenario, we’re interested in understanding the relationship between two variables.
One of the most common ways to quantify a relationship between two variables is to use the Pearson correlation coefficient, which is a measure of the linear association between two variables.
It always takes on a value between -1 and 1 where:
- -1 indicates a perfectly negative linear correlation between two variables
- 0 indicates no linear correlation between two variables
- 1 indicates a perfectly positive linear correlation between two variables
Often denoted as r, this number helps us understand the strength of the relationship between two variables. The closer r is to zero, the weaker the relationship between the two variables.
It’s important to note that two variables could have a weak positive correlation or a weak negative correlation.
Weak positive correlation: When one variable increases, the other variable tends to increase as well, but in a weak or unreliable manner.

Weak negative correlation: When one variable increases, the other variable tends to decrease, but in a weak or unreliable manner.
The following table shows the rule of thumb for interpreting the strength of the relationship between two variables based on the value of r:
| Absolute value of r | Strength of relationship |
|---|---|
| r | No relationship |
| 0.25 | Weak relationship |
| 0.5 | Moderate relationship |
| r > 0.75 | Strong relationship |
The correlation between two variables is considered to be weak if the absolute value of r is between 0.25 and 0.5.
However, the definition of a “weak” correlation can vary from one field to the next.
Medical
In medical fields the definition of a “weak” relationship is often much lower. If the relationship between taking a certain drug and the reduction in heart attacks is r = 0.2, this might be considered “no relationship” in other fields, but in medicine it’s significant enough that it would be worth taking the drug to reduce the chances of having a heart attack.
Human Resources
In a field like human resources, lower correlations are also used more often. For example, the correlation between college GPA and job performance has been shown to be about r = 0.16. This is fairly low, but it’s large enough that it’s something a company would at least look at during an interview process.
Technology
In technology fields, the correlation between variables might need to be much higher to even be considered “weak.” For example, if a company creates a self-driving car and the correlation between the car’s turning decisions and the probability of avoiding a wreck is r = 0.95, this may be considered a “weak” correlation and is likely too low for the car to be considered safe since the result of making the wrong decision can be fatal.
Using Scatterplots to Visualize Correlations
When you calculate the correlation coefficient between two variables, it’s useful to create a scatterplot to visualize the correlation as well.
In particular, scatterplots offer two benefits:
1. Scatterplots can help you identify outliers that affect the correlation coefficient.
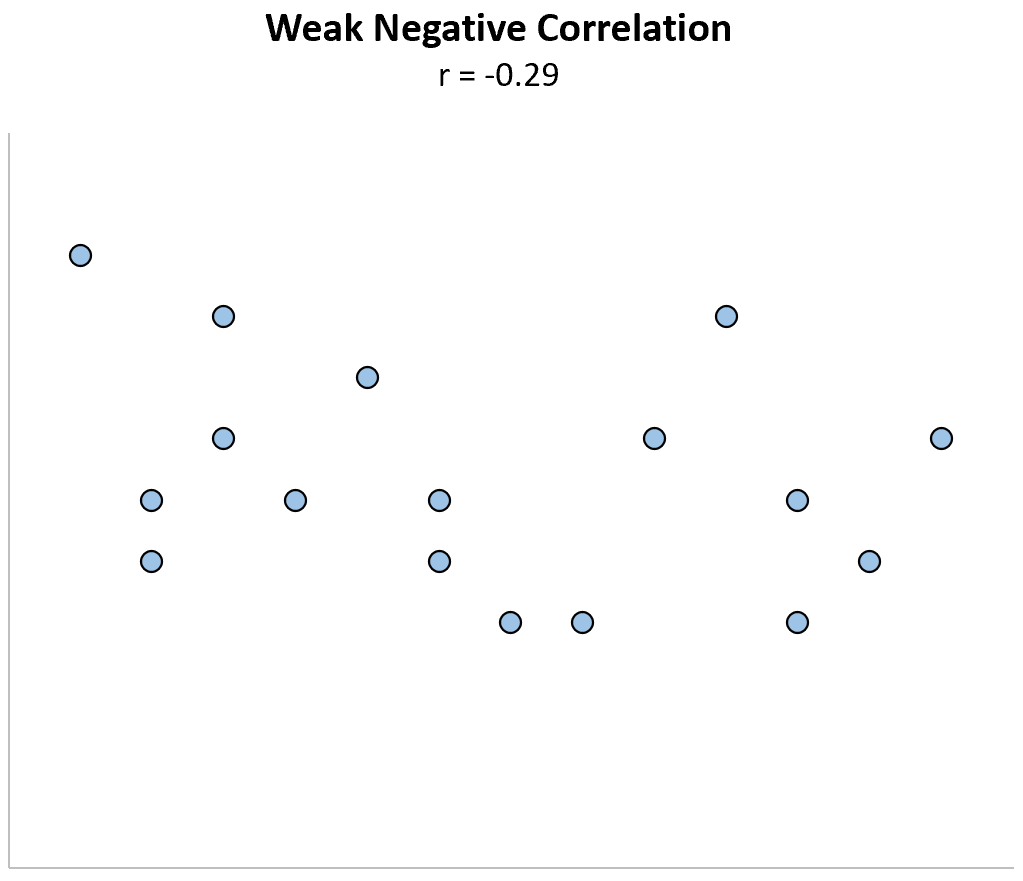
One extreme outlier can have a large impact on the correlation coefficient. Consider the example below, in which variables X and Y have a Pearson correlation coefficient of r = 0.91.

Now imagine that the we modify the first data point to be much larger. The correlation coefficient suddenly becomes r = 0.29.

This single data point causes the correlation coefficient to change from a strong positive relationship to a weak positive relationship.
(2) Scatterplots can help you identify nonlinear relationships between variables.
A Pearson correlation coefficient merely tells us if two variables are linearly related. But even if a Pearson correlation coefficient tells us that two variables are uncorrelated, they could still have some type of nonlinear relationship.
For example, consider the scatterplot below between variables X and Y, in which their correlation is r = 0.00.
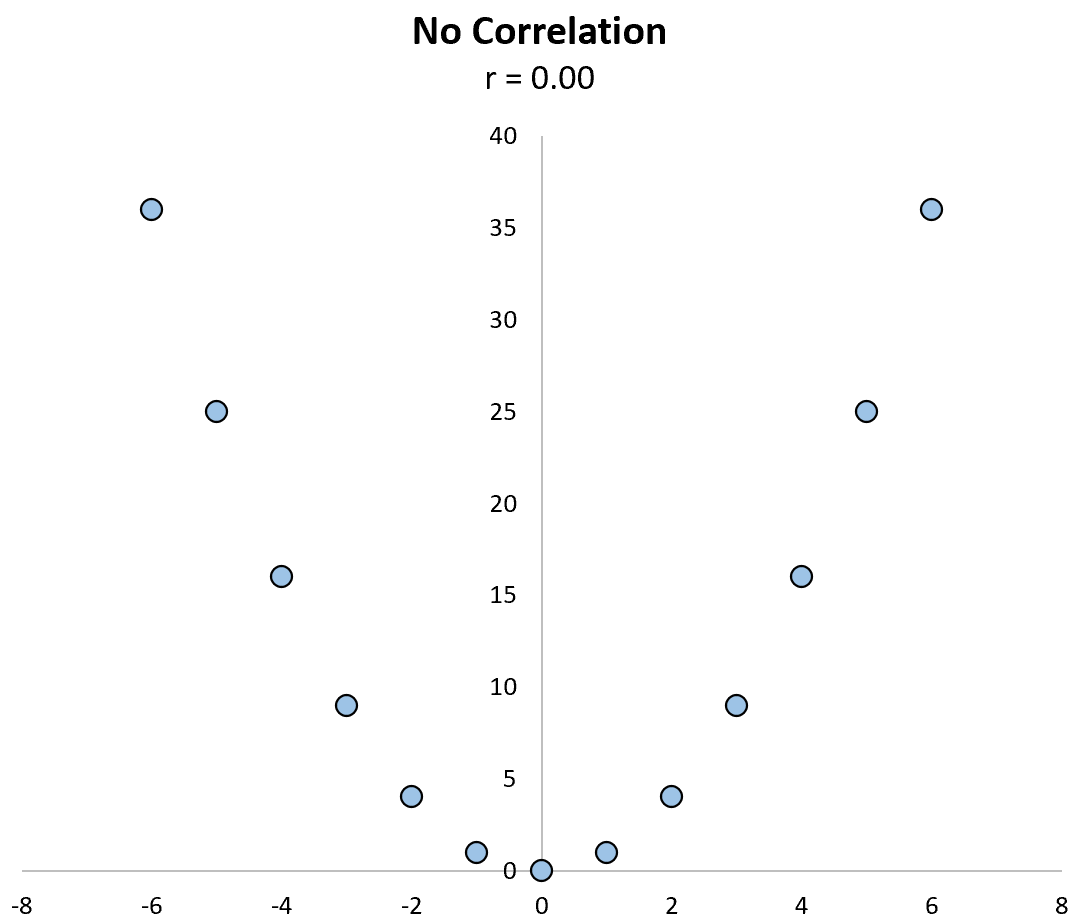
The variables clearly have no linear relationship, but they do have a nonlinear relationship: The y values are simply the x values squared.
A correlation coefficient by itself couldn’t pick up on this relationship, but a scatterplot could.
Conclusion
In summary:
1. As a rule of thumb, a correlation coefficient between 0.25 and 0.5 is considered to be a “weak” correlation between two variables.
2. This rule of thumb can vary from field to field. For example, a much lower correlation could be considered weak in a medical field compared to a technology field. Be sure to use subject matter expertise when deciding what is considered to be a weak correlation.
3.When using a correlation coefficient to describe the relationship between two variables, it’s useful to create a scatterplot as well so you can identify any outliers in the dataset along with a potential nonlinear relationship.
Additional Resources
What is Considered to Be a “Strong” Correlation?
Correlation Matrix Calculator
Correlation vs. Association: What’s the Difference?
