Proof of De Morgan’s Law
De Morgan’s Law states that how mathematical statements and concepts are related through their opposites. In set theory, De Morgan’s Laws describe the complement of the union of two sets is always equals to the intersection of their complements. And the complement of the intersection of two sets is always equal to the union of their complements. In this article, we will learn how to prove De Morgan’s Law with some examples. We can also use De Morgan’s Laws in computer engineering in Boolean Logic.
De Morgan’s Laws Statement and Proof
Before proceedings to De Morgan’s Laws, first, we need to understand is what is set? As the name suggests set is the well-defined collection of objects or elements. De Morgan’s laws are very simple and easy to understand. It consists of different operations such as union, intersection, and complement of a set that can be performed on two sets. In a universal set, we consider all the objects or elements related to a specific context. The universal set is represented as U.
Let’s understand this concept with the help of an example; Consider a universal set U, and the subset of the universal set is A and B.
For any two finite sets A and B
1) De Morgan’s law of union
= (A ∪B)’ = A’ ∩ B’
2) De Morgan’s law of intersection
= (A ∩B)’ = A’ ∪ B’
De Morgan’s law of union
= (A ∪B)’ = A’ ∩ B’ ……… (1)
Where complement of a set is given as
A’ = { x:x ∈ ∪and x ∉A}
Where,
A’ = It denotes the complement
We can easily understand this concept with the help of Venn Diagrams.
The left-hand side of the first equation produces the complement of both sets A and B. It means the union of set A and B is the set of all elements that lie either in Set A or in Set B. The given diagram depicts the Venn diagram of set A and Set B.

In the above diagram, the highlighted blue color area represents the A. The complement of (A)’ is a set of all those elements except the highlighted blue color area. The given diagram depicts the Venn diagram of the complement of A and B.

Similarly, the right-hand side of the first equation can be represented by the given Venn Diagram. The given diagram depicts the complement of A.

The green part represents Set A, and the yellow part represents its complement that is A.’
Similarly, the component of B can be represented as
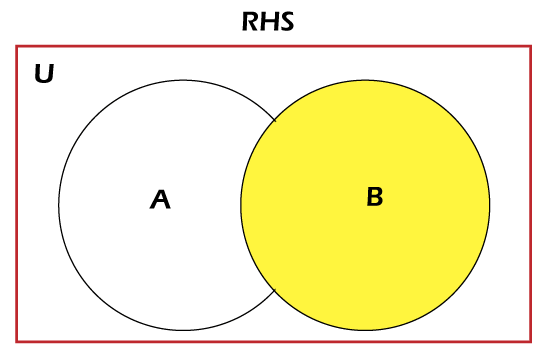
The yellow part represents the set B, and the White part indicates its complement: B.’
Now, we will be combined both the image 3 and 4 to one another, we get the given Venn Diagram

Therefore,
L.H.S = R.H.S
Mathematically,
A ∪B = Either A or B
(A ∪B)’ = Neither A nor B
A’ = Not lies in A
B’ Not lies in B
A’ ∩B’ = Not in A and not in B.
Let J = (A U B)’ and K= A’ ∩ B.’
Let’s s be an arbitrary element of J then s ∈ J = s ∈ (A U B).’
= s ∉ (A U B)
= s ∉ A and s ∉ B
= s ∈ A’ and s ∈ B.’
= s ∈ A’ ∩ B.’
= s ∈ K
Therefore, J ⊂ K ………(i)
Again, let t be an arbitrary element of K then t ∈ K = t ∈ A’ ∩ B.’
= t ∈ A’ and t ∈ B.’
= t ∉ A and t ∉ B
= t ∉ (A U B)
= t ∈ (A U B).’
= t ∈ J
Therefore, K ⊂ J ………… (ii)
Now combine (i) and (ii) we get; J = K i.e. (A U B)’ = A’ ∩ B’
Therefore, by applying Venn Diagrams and Analyzing De Morgan’s Laws, we have proved that (A)’ = A’ ∩B.’
De Morgan’s theorem describes that the product of the complement of all the terms is equal to the summation of each individual term’s component.
Proof of De Morgan’s law:
(A ∩ B)’ = A’ U B.’
Let P = (A ∩ B)’ and Q = A’ U B’
Let’s s be an arbitrary element of M then s ∈ P = s ∈ (A ∩ B).’
= s ∉ (A ∩ B)
= s ∉ A or x ∉ B
= s ∈ A’ or s ∈ B.’
= s ∈ A’ U B.’
= s ∈ N
Therefore, P ⊂ Q …………(i)
Again, let t be an arbitrary element of Q then t ∈ N = t ∈ A’ U B.’
= t ∈ A’ or t ∈ B.’
= t ∉ A or t ∉ B
= t ∉ (A ∩ B)
= t ∈ (A ∩ B).’
= t ∈ M
Therefore, Q ⊂ P…………(ii)
Now combine (i) and (ii) we get; P = Q i.e. (A ∩ B)’ = A’ U B’
Questions based on De Morgan’s Law
Question 1:
If U = {2, 3, 4, 5, 6, 7, 8, 9}, A = {5,6,7} and B = {6,7,9}. Show that
(A ∪ B)’ = A’ ∩ B’.
Solution:
We know that,
U = {2, 3, 4, 5, 6, 7, 8, 9}
A = {5, 6, 7}
B = {6, 7, 9}
A ∪ B = {5, 6, 7} ∪ {6, 7, 9}
= {5, 6, 7, 9}
Therefore, (A ∪ B)’ = {2, 3, 4, 8} ……………… (i)
Now, A = {5, 6, 7} so, A’ = {2, 3, 4, 8, 9}
And, B = {6, 7, 9} so, B’ = {2, 3, 4, 5, 8}A’ ∩ B’ = {2, 3, 4, 8, 9} ∩ {2, 3, 4, 5, 8}
Therefore, A’ ∩ B’ = {2, 3, 4, 8 } ……………… (ii)
Combining equation (i) and (ii) we get;
(A ∪ B)’ = A’ ∩ B’
Question 2:
If U = {a, b, c, d, e}, P = {a, b, c} and Q = {b, c, e}.
Proof of De Morgan’s law: (P ∩ Q)’ = P’ U Q’.
Solution:
We know that,
U = {a, b, c, d, e}
P = {a, b, c}
Q = {b, c, e}
(P ∩ Q) = {a, b, c} ∩ {b, c, e}/p>
= {b, c}
Therefore, (P ∩ Q)’ = {a, d, e} …………(i)
Again, P = {a, b, c} so, P’ = {d, e}
and Q = {b, c, e} so, Q’ = {a, d}
P’ ∪ Q’ = {d, e} ∪ {a, d}
Therefore, P’ ∪ Q’ = {a, d, e} ……………….. (ii)
Combining equations (i) and (ii), we get;
(P ∩ Q)’ = P’ U Q’.
Question 3:
If U = {1, 3, 5, 6, 7, 9, 11, 13}, A = {5, 7, 11} and B = {7, 11, 13}. Show that
(A ∪ B)’ = A’ ∩ B’.
Solution:
We know that,
U = {1, 3, 5, 6, 7, 9, 11, 13}
A = {5, 7, 11}
B = {7, 11, 13}.
A ∪ B = {5, 7, 11} ∪ {7, 11, 13}.
= {5, 7, 11, 13}
Therefore,
(A ∪ B)’ = {1, 3, 6, 9} ……………… (i)
Now A = {5, 7, 11}
so, A’ = {1, 3, 6, 9, 13}
And, B = {7, 11, 13}. so, B’ = {1, 3, 5, 6, 9}
A’ ∩ B’ = {1, 3, 6, 9, 13} ∩ {1, 3, 5, 6, 9}
Therefore, A’ ∩ B’ = {1, 3, 6, 9} ……………(ii)
Combining equation (i) and (ii) we get;
(A ∪ B)’ = A’ ∩ B’
Question 4:
If U = {p, q, r, s, t}, A = {p, q, r} and B = {q, r, t}.
Proof of De Morgan’s law: (A ∩ B’ = A’ U B’.
Solution:
We know that,
U = {p, q, r, s, t}
A = {p, q, r}
B = {q, r, t}.
(A ∩ B) = {p, q, r} ∩ {q, r, t}
= {q, r}
Therefore, (A ∩ B)’ = {p, s, t} ………… (i)
Again, A = {p, q, r} so, A’ = {s, t}
And, B = {q, r, t}
so, B’ = {p, s} A’ ∪ B’ = {s, t} ∪ {p, s}
Therefore,
A’ ∪ B’ = {p, s, t} …………… (ii)
Combining equations (i) and (ii), we get;
(A ∩ B)’ = A’ U B’.
